この記事の目的
通常のコンピュータでは、記録ビットに生じるエラーを減らすために、1ビットに記録する情報をON/OFFの2値に制限している。それに対して量子コンピュータは、1量子ビットに、 \(\alpha\left|0\right\rangle+\beta\left|1\right\rangle\) (\(\alpha^2+\beta^2=1\))の形で多値のデータを記録する。これにより(及びn量子ビットに2nのデータを記録できることにより)、いくつかの問題に対しては、通常のコンピュータに比べて圧倒的に高速に解くことができるとされている。
量子ビットは、古典的ビットに比べてエラーに強いわけではない。多値データを記録すれば、当然上式の \(\alpha, \beta\) の微小な変化(位相回転等)がエラーになり、計算結果には誤りが生じることになる。
ところが、量子ビットでは、通常の記録ビットにはない強力なエラー訂正技術を使うことができる。すなわち、ビット反転と位相反転のエラー訂正ができれば、あらゆる量子アナログエラーから護ることができる*。この、量子ビットに特有なエラー訂正技術のために、1量子ビットに多値のデータを記録することが可能になり、量子コンピュータによる高速計算が実現可能だと考えられている。
*たとえば、[1]の10.2。「Shorの符号は単一qビットに対するビット反転と位相反転以上の誤りから守ることができる」「単一qビットに働く限り任意の誤りから完全に護る」
本記事では、Shorの符号や表面符号等、ビット反転と位相反転のエラー訂正の技術(例えば[2]の6章)については知識があることを前提にして、この二つができると任意の(1量子ビットの)量子アナログエラーから護ることができる理由をまとめる。
これは、[2]の6.3の「エラーを記述できる演算子ε1は(中略)$$ℇ_1=e_0 I+e_1 X_1+e_2 Z_1+e_3 X_1 Z_1$$という形に書けます」の、(おそらく紙面の都合で説明が省略されてしまった)ε1とは何か、ということでもある。
●本記事は、エラーを記述できる演算子の導出と、量子アナログエラー訂正に関するものだが、これは、[1]では2章「量子力学入門」の一部、8章「量子雑音と量子演算」、10章「量子誤り訂正」の一部にまたがる長いストーリーになっている。本記事の中では、個々の定理等についての証明には立ち入らず、それらの定理の意味、関係をつかむための説明、例示等によって、全体の構成を[1]をベースに読み解きたい。
参考文献
[1] 量子コンピュータと量子通信 Nielsen, Chuang オーム社
[2] 量子コンピューティング 嶋田義皓 オーム社
[3] Quantum error correction below the surface code threshold, Google Quantum AI and Collaborators, arXiv:2408.13687 [quant-ph], https://arxiv.org/abs/2408.13687
[4] (初出文献ではなく、参考文献として)Khatri, S., Sharma, K., & Wilde, M. (2020). Information-theoretic aspects of the generalized amplitude damping channel. Physical Review A, 102 (1), 1903.07747
密度オペレータ
量子力学では、熱緩和した状態のように、お互いに位相関係がない多くの状態の混合状態を取り扱うことがある。混合状態は純粋状態のように状態ベクトルでは表せないが、下表のように密度オペレータ*によって、確率piで現れる純粋状態\(\left|\psi_i\right\rangle\left\langle\psi_i\right|\)の和として書き表し、期待値等を計算することができる。
| 純粋状態 | 混合状態 | |||
| 状態ベクトル | 密度行列 | 状態ベクトル | 密度行列 | |
| 状態 | \(|\psi\rangle\) | \(\rho=\left|\psi\right\rangle\left\langle\psi\right|\) | - | \(\rho=\sum_{i}{p_i\left|\psi_i\right\rangle\left\langle\psi_i\right|}\) |
| 時間発展 | \(\left|\psi’\right\rangle=U\left|\psi\right\rangle\) | \(\rho’=U\rho U^{-1}\) | - | \(\rho’=U\rho U^{-1}\) |
| Aの期待値 | \(\left\langle\psi\right|A\left|\psi\right\rangle\) | \(\mathrm{tr}\left(\rho A\right)\) | - | \(\mathrm{tr}\left(\rho A\right)\) |
*本記事では、密度オペレータ(=密度行列)についての知識は前提としている(たとえば、[1]の2.4参照)が、本記事で必要な密度オペレータの知識について、いくつか挙げる。
〇 \(|\_\rangle\langle\_|\)という形式について
例えば、左側のケットベクトルが\(\psi\)、右側が\(\varphi\)という状態であれば、\(|\psi\rangle\langle\varphi|\)となり、これに右から\(\left|\varphi\right\rangle\)を作用させれば、\(\left|\psi\right\rangle\left\langle\varphi\middle|\varphi\right\rangle=\left|\psi\right\rangle\)(\(\left|\varphi\right\rangle\)と\(\left|\varphi\right\rangle\)の内積は1なので)。従って、\(|\psi\rangle\langle\varphi|\)は\(\left|\varphi\right\rangle\)を\(\left|\psi\right\rangle\)に変換する線形オペレータである。
〇 密度オペレータの表現行列(密度行列)
\(\left|\psi\right\rangle=\alpha\left|0\right\rangle+\beta\left|1\right\rangle\)(純粋状態)の場合、\(\rho=\left|\psi\right\rangle\left\langle\psi\right|\)は\(\left|\psi\right\rangle\left\langle\psi\right|=\left(\alpha\left|0\right\rangle+\beta\left|1\right\rangle\right)\left(\alpha^\ast\left\langle0\right|+\beta^\ast\left\langle1\right|\right)=\left|\alpha\right|^2\left|0\right\rangle\left\langle0\right|+\alpha\beta^\ast\left|0\right\rangle\left\langle1\right|+\alpha^\ast\beta\left|1\right\rangle\left\langle0\right|+\left|\beta\right|^2\left|1\right\rangle\left\langle1\right|\)と展開できる。これは、\(\rho=\left|\psi\right\rangle\left\langle\psi\right|\)という線形オペレータが、\(\left|0\right\rangle,\ \left|1\right\rangle\)を基底として、\(\left[\begin{matrix}\left|\alpha\right|^2&\alpha\beta^\ast\\\alpha^\ast\beta&\left|\beta\right|^2\\\end{matrix}\right]\)と行列表現できることを意味する。
〇量子雑音による純粋状態から混合状態への移行を密度行列で表す([1]の8.3.6)
量子ビットの純粋状態では、上記のように\(\left|\psi\right\rangle\)は\(\left|0\right\rangle\)と\(\left|1\right\rangle\)の線形結合で結ばれており、純粋状態であることは、密度行列では、上記のように非対角項がある(正確に言うと、非対角項により、\(\mathrm{tr}\left(\rho^2\right)=1\)になる)ことに現れる。この純粋状態は、\(\left|0\right\rangle\)と\(\left|1\right\rangle\)の間のランダムな位相ノイズ\(R_z\left(\theta\right)\)(θはランダム)を何度も受けるうちに位相関係に乱れが生じて(=非対角項が小さくなり)、最終的に\(\left[\begin{matrix}\left|\alpha\right|^2&0\\0&\left|\beta\right|^2\\\end{matrix}\right]\) となる(横緩和)。この状態は、\(\left|\alpha\right|^2\left|0\right\rangle\left\langle0\right|+\left|\beta\right|^2\left|1\right\rangle\left\langle1\right|\)と書くことができ、\(\left|0\right\rangle\)と\(\left|1\right\rangle\)の混合状態になっていることがわかる。このように、密度行列は純粋状態、混合状態をシームレスに記述することができるため、量子雑音、量子エラーの記述には、密度行列が必須になる。
〇密度オペレータ(または密度行列)ρの一般的性質
ρは、状態の確率piの合計が1であることから、\(tr\left(\rho\right)=1\) 、かつ、確率piが負にならないことから、正値オペレータである([1]の2.4.1)。
この密度オペレータを利用すると、(量子エラーの原因になる)外場があるときの、対象とする量子ビットに関する時間発展を記述することができる。
ここからは、(時間発展に伴う)エラーの発生前後の状態変化に注目するため、始状態から終状態への時間発展のことを、「状態変化」という用語で表現する。
対象の系の状態変化:全系がわかっているとき
準備:対象の系の密度オペレータ
2個の系(例えば2個の量子ビット)A、Bの状態を\(\rho^{AB}\)とする。このときのAの状態\(\rho^{A}\)は、系Bでの部分トレースにより、
\(\rho^A\equiv{\mathrm{tr}}_B\left(\rho^{AB}\right)\) (1)
になる。*
*[1]の(2.177)式。等号ではなく、定義式(≡)になっていることに注意。\(\rho^{AB}\)のBによる部分トレースが、物理量Xを\({\mathrm{tr}}\left({\mathrm{tr}}_B\left(\rho^{AB}\right)X\right)\)で計算可能であるということを証明して、\(\rho^{A}\)と同等であると結論づけている。([1]のコラム2.6)。
念のため:\(\rho^{AB}\)は、2個の量子ビットの系であれば、基底\(\left|00\right\rangle,\ \left|01\right\rangle,\left|10\right\rangle,\ \left|11\right\rangle\)を使って、4次行列、\(\rho^{A}\)は、Bの部分だけトレースをとるので、2次行列になる。
対象の系の状態変化
(1)式を使うと、\(\rho^{AB}\)の状態変化がUで表されるとき、\(\rho^{A}\)は、Uによって\(\mathcal{E}\left(\rho^{A}\right)={\mathrm{tr}}_{\mathrm{B}}\left[U\rho^{AB}U^{\dagger}\right]\)となる。特に、対象の系と外場が直積になっている(\(\rho\otimes\rho_{\mathrm{env}}\))*とすると、ρの状態変化は、
\(\mathcal{E}\left(\rho\right)={\mathrm{tr}}_{\mathrm{env}}\left[U\left(\rho\otimes\rho_{\mathrm{env}}\right)U^{\dagger}\right]\) (2)
*通常は、外場とρが直積状態になっているわけではなく、様々な相互作用を介して熱平衡状態になっている。しかし量子ビットのような系では、初期化を行うため、ρは初期状態ではいったん外場との相互作用の影響がない(=直積の関係にある)純粋状態になる。([1]の8.2.2)
さらに、\(\rho_{\mathrm{env}}=\left|e_0\right\rangle\left\langle e_0\right|\)として 外場の状態空間の正規直交基底\(\left|e_k\right\rangle\)で展開すると
\(\mathcal{E}\left(\rho\right)=\sum_{k}{E_k\rho E_k^{\dagger}}\ \ \ \left(E_k=\left\langle e_k\middle| U\middle| e_0\right\rangle\right)\) * (3)
これはεのオペレータ表現と呼ばれる([1]の(8.10))。外場との相互作用をするρの状態変化の基本式になる。
*外場を\(\left|e_0\right\rangle\)としているが、これは、一般的には\(\left|e_0\right\rangle\)は外場を基底状態等の特定の状態にセットした、という意味ではない(外場は通常混合状態(ふつうは熱平衡状態)なので)
ただし、d次元空間内の外場は通常混合状態だが、付加的なd次元のシステムを付け加えたd2次元内で、その混合状態を純粋状態にすることができる(純粋化([1]の式(8.9)の上の説明参照))。この純粋状態を\(\left|e_0\right\rangle\)とする正規直交基底により、(3)式のように書くことができる。\(\left|e_0\right\rangle\) にも、それに続く\(\left|e_k\right\rangle\)にも特に物理的な意味はなく(実際の系とは関係ない付加システムを付け加えてしまったので)、単に、外場がある場合の状態変化は、ある線形オペレータEkとEk†を両側からかけて、複数個の足し算をした形で表すことができるという、(3)式の「カタチ」を示している。
実際、[1]の定理8.1で、(3)式は、特定の外場を想定しなくても、密度オペレータを密度オペレータに移す線形写像に自然に課される条件から導出できることが示される。従ってその場合は、Ekには \(E_k=\left\langle e_k\middle| U\middle| e_0\right\rangle\) のような紐づけはない。
外場のない状態では、ρの状態変化は \(U\rho U^{\dagger}\) と表され、合計の確率が保存される(\(\mathrm{tr}\left(\mathcal{E}\left(\rho\right)\right)=1\))条件から、Uはユニタリ変換という制限がつく。外場がある場合は、この条件は、Ek(以下、演算要素と呼ぶ)に対する、
\(\sum_{k}{E_kE_k^{\dagger}}=I\) (4)
(完全性)という条件になる([1]の(8.14))。演算要素が1個だけの場合は、この式は外場がない場合のユニタリ変換の条件そのものになる。
また、状態変化を表すのに必要なEk の個数については、対象の系の次元がdのとき、d2以下でよいこともわかっている([1]の定理8.3)。対象の系が量子ビットなら、d=2なので、d2=4個以下で表すことができることになる。
上記の(3), (4)式によって、外場がある場合(ない場合を含む)の対象の系の状態変化を表すことができるが、このオペレータ和表現の式は、あまりシンプルではなく、すぐに腑に落ちる式でもないと思われるので、「補遺」で、具体的な姿を示す。必要なEkの個数についても「補遺」の最後に追記する。
EkはI,X,Y,Zに分解できる
準備:2次行列の正規直交基底による展開
量子ビットのような2次元Hilbert空間上の線形オペレータEkは、適当な正規直交基底により2次行列として表される。この行列は、22の独立な要素を持つベクトルと見ることもできる。実際、2次行列は \(\mathrm{tr}\left(A^{\dagger}B\right)\)のような内積(Hilbert-Schmidt内積)を定義することができるので、22次元のHilbert空間の要素と考えることができる。\(\frac{I}{\sqrt2},\ \frac{X}{\sqrt2},\ \frac{Y}{\sqrt2},\ \frac{Z}{\sqrt2}\)はこの内積での正規直交基底なので、2次行列はI,X,Y,Zの線形結合として、
\(E_k=\frac{\mathrm{tr}\left(E_k\right)I+\mathrm{tr}\left(X E_k\right)X+\mathrm{tr}\left(Y E_k\right)Y+\mathrm{tr}\left(Z E_k\right)Z}{2}\) (5)
と一意的に表すことができる([1]の式(8.148)。ただし、(8.148)はρについての式になっている。)。
測定による誤りの離散化
純粋状態に初期化された量子ビット\(\rho=\left|\psi\right\rangle\left\langle\psi\right|\)に、エラーを引き起こす状態変化が生じる(\(\rho\rightarrow\mathcal{E}\left(\rho\right)\))と、(3)式のような混合状態(各項は純粋状態だが、各項の間には位相関係はない)になる。(純粋状態である)各項は\(\left|\psi\right\rangle\rightarrow E_k\left|\psi\right\rangle\)という変換を受けている*。Ekは、(5)式のようにI,X,Y,Zに分解することができる。
すると、状態変化が生じた後に測定を行う(測定の行い方は補遺参照)ことにより、ある確率でいずれかの項が選択され、そのEkに対して、状態は\(\left|\psi\right\rangle\)(エラーなし)、 \(X\left|\psi\right\rangle\)(ビット反転)、\(Z\left|\psi\right\rangle\)(位相反転)、\(Y\left|\psi\right\rangle=iXZ\left|\psi\right\rangle\)(ビット、位相反転)のいずれかに収縮する。測定結果に従ってエラー訂正をすることで、\(\left|\psi\right\rangle\)に戻ることになる。**
*念のため:[3]の6.3節の「エラーを記述する演算子」は、特に説明なく出てくるが、上記のEkということになる。
**生じうる全てのエラーは(3)式で表され、そのEkがわずか4個のエラーパターン(I,X,Y,Z)の線形結合で表され、測定によって4個のエラーパターンのいずれかに収縮する。従ってどのようなアナログエラーが生じても、ビット反転と位相反転(と、その掛け算)を検出(=収縮)して、修正するだけで元に戻すことができる。魔法のようなストーリーだが、Google [3] が現実に、この量子エラー訂正により量子ビットの寿命を延ばすことに成功している。測定による収縮という量子力学の根幹の部分(最も不思議な部分の一つ)を技術的に応用してしまうときが来たことになる…
補遺 オペレータ和表現の例と、それによるエラー訂正
本記事では、エラーを引き起こす状態変化の一般的な定式化と、この定式化から、エラーはビット反転と位相反転の合成として表すことができ、エラー訂正が可能になることについて、アウトラインを示した。
しかし、その中心になるオペレータ和表現は、ユニタリ変換に比べて、あまりシンプルではなく、すぐに腑に落ちる式でもないと感じる。例えば、一番シンプルな例として、励起状態|1>から基底状態|0>に落ちてしまう、寿命T1に関わるエラーは、このオペレータ和表現を使ってどのように表されるのか*、また、そのエラーは具体的にどのようにして検出、訂正できるのか。[1]の8.3.5の、振幅ダンピング(Amplitude Damping)と呼ばれる量子演算(状態変化)を例にとって、説明する**。
*2準位系に外からπパルスを与えると(演算子Yに相当)、|1>は|0>になるが、|0>も|1>になる。一方、下記[1]の8.3.5で振幅ダンピングとして紹介されるエラーは、励起状態|1>から基底状態|0>に落ちるが、基底状態|0>が|1>になることはない。このような、ユニタリ変換では表すことができない変換(エラー)をオペレータ和表現では、表すことができる。
**[1]では、本量子演算は2個の光子モードに関するものとして説明されている。光子モードだけでなく、電子の励起準位からの光子の自然放出も同じモデルで表すことができる([1]の演習8.24)が、筆者のイメージする、量子ビットが他の欠陥等の2準位系(または隣の量子ビット)とカップルしてT1エラーを引き起こす、というような機構とは違うようである。本節ではこの量子演算を、外場まで含めたエラーのモデル(ユニタリ変換)から、オペレータ和表現への変換、エラー訂正までの手順の説明のための一例として取り上げる。
[1]の8.3.5では、二つの光子モードのビームスプリッタによる結合について説明されている。
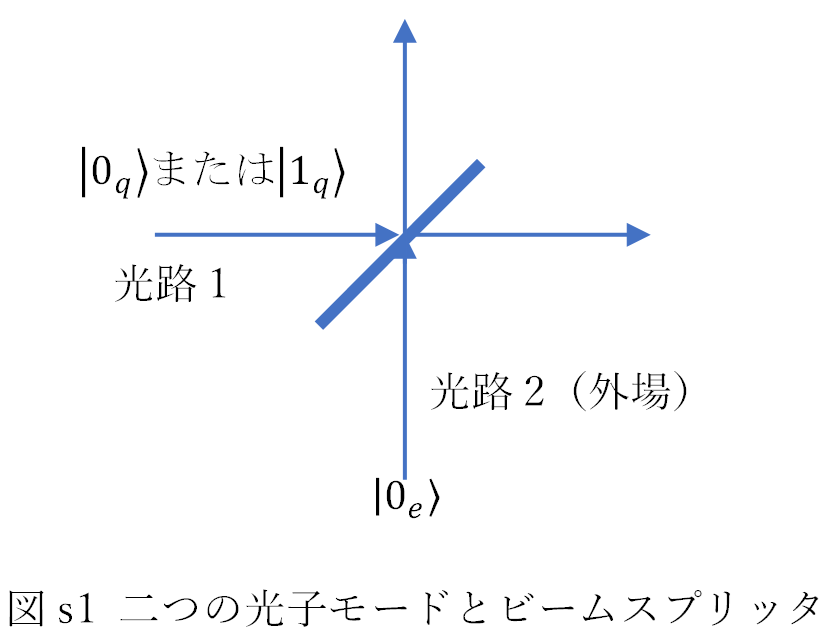
この例では、図s1のように、2本の光路の一方に注目して(光路1=対象の光路)、他方の光路(外場)には初期状態で光子がない(\(\left|0_e\right\rangle\))場合に、ビームスプリッタ通過後の、対象の光路の状態を計算している。
2本の光路とビームスプリッタの全系では、ビームスプリッタの前後での光子の挙動はユニタリ変換\(B=\exp{\left[\theta\left(a^{\dagger}b-ab^{\dagger}\right)\right]}\)([1]の(7.25))で表される。
Bの表式はわかりにくいが結果は直感的にわかりやすい。
$$B\left|0_e0_q\right\rangle=\left|0_e0_q\right\rangle$$$$B\left|0_e1_q\right\rangle=\cos{\theta}\left|0_e1_q\right\rangle+\sin{\theta}\left|1_e0_q\right\rangle$$([1]の(7.34)等より。ケットベクトル内は、外場の光路、対象の光路の順であることに注意)
それぞれ、どちらにも光子がない場合はビームスプリッタを通過しても光子はない、対象の光路にあった光子は、ビームスプリッタの(いわば)透過率cosθ、反射率sinθの二乗の確率でどちらかの光路に存在する、ことを意味する*。
*マクロな(量子的でない)光ビームの透過率、反射率に対する表記と全く同じだが、ビームスプリッタは、光子に対しては対象の光路と外場の光路を結合して、\(\left|{0_e1}_q\right\rangle\rightarrow\alpha\left|{0_e1}_q\right\rangle+\beta\left|{1_e0}_q\right\rangle\) のように2個の固有状態の重ね合わせに変換する役割を持つ(光ビームを量的に分割するのとは違い、光子は分けられないので)。測定を行うと、\(\left|\alpha\right|^2,\left|\beta\right|^2\) の確率で\(\left|{0_e1}_q\right\rangle\) か\(\left|{1_e0}_q\right\rangle\) に収縮する。
このような全系の状態変化をオペレータ和表現で書き直す。
対象の光路に対するEkを計算するために、このBを行列で書くと、
$$\begin{matrix}\ &\begin{matrix}\left\langle00\right|&\left\langle01\right|\\\end{matrix}\\\begin{matrix}\left|00\right\rangle\\\left|01\right\rangle\\\left|10\right\rangle\\\left|11\right\rangle\\\end{matrix}&\left[\begin{matrix}1\ \ \ &0\\0\ \ \ &\cos{\theta}\\0\ \ \ &\sin{\theta}\\0\ \ \ &0\\\end{matrix}\right]\\\end{matrix}$$
のようになる。(\(E_0=\left\langle0_e\middle| B\middle|0_e\right\rangle\)、\(E_1=\left\langle1_e\middle| B\middle|0_e\right\rangle\)*の計算に必要な部分だけ表記している**)
*\(\left|0_e\right\rangle\)はこの場合、純粋化によって人工的に作られた純粋状態ではなく、光子数0の純粋状態(初期状態では外場に光子がない場合を想定している)。従って、ここでのEkは、物理的に意味のある状態で挟まれており、物理的な意味(外場の光子数が0から1になる、等)を持つ。
**Bは実際には光子数状態に対する\(\left|mn\right\rangle\ (m,n=0,1,2,\cdots)\) の無限次元の正規直交基底で展開される。外場に光子がなく(\(\left|0_e\right\rangle\))、対象の光路が\(\left|0_q\right\rangle, \left|1_q\right\rangle\)の重ね合わせである初期状態から開始した場合だけはm,nが2以上にならず、二準位系から外場にエネルギーが放出されるような状態変化を表すことができる。
すると、\(E_0=\left[\begin{matrix}1&0\\0&\cos{\theta}\\\end{matrix}\right]\)、\(E_1=\left[\begin{matrix}0&\sin{\theta}\\0&0\\\end{matrix}\right]\)となり、このE1, E2を使って、対象の光路の状態ρは
\(\mathcal{E}\left(\rho\right)=E_0\rho E_0^{\dagger}+E_1\rho E_1^{\dagger}\) (s1)
となる*。
*この2項だけで、(4)式の完全性の条件を満たす。
始状態で対象の光路に光子が1個ある(\(\left|1_q\right\rangle\))とすれば、\(\rho=\left[\begin{matrix}0&0\\0&1\\\end{matrix}\right]\)なので、
\(\mathcal{E}\left(\rho\right)=\cos^2{\theta}\left[\begin{matrix}0&0\\0&1\\\end{matrix}\right]+\sin^2{\theta}\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]\) (s2)
となる。全系ではユニタリ変換により純粋状態に変換されるが、対象の光路だけを見た場合は\(\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]\)と\(\left[\begin{matrix}0&0\\0&1\\\end{matrix}\right]\)の混合状態になる。初期状態で\(\left[\begin{matrix}0&0\\0&1\\\end{matrix}\right]\)だったものが、sin2θの確率で基底状態\(\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]\)に落ちることになる。(s1)と(s2)を見比べると原因ははっきりしていて、外場の光路に光子が移ったから(\(E_1=\left\langle1_e\middle| B\middle|0_e\right\rangle\)の変換が起こったから)、ということになる。(始状態が\(\left|0_q\right\rangle\)のときは、\(\rho=\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]\) なので、(s1)の第2項は0になるため、\(\mathcal{E}\left(\rho\right)=\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]\)のまま。)
ここまで、オペレータ和表現の具体的な形を一つの例で示した。このように\(\mathcal{E}\left(\rho\right)\)を計算することは、終状態での期待値を求める上では必要な作業である。
しかし、エラーの検出、訂正は、期待値のような、繰り返し測定による統計的な結果ではなく、単一の事象に対する操作になる。従って、エラー検出と訂正は、ある確率で実現する\(\mathcal{E}\left(\rho\right)\)のそれぞれの項(純粋状態)について、行う必要がある。
この手順について、E1によるエラーが起こったとして以下で説明する。
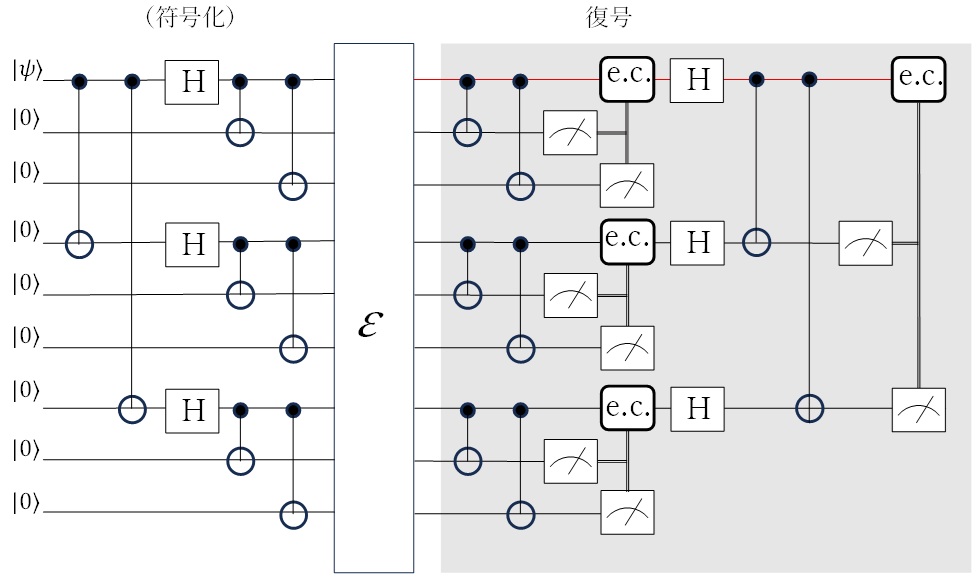
本記事では、Shorの符号*で符号化された論理ビットについて、図s2のようにエラー訂正を行うことにする。図s2ではパリティーチェックは[2]の図6.2と同様に行うが、エラー検出は測定により行い、測定結果に応じてI, X, Zを演算することによりエラー訂正を行う**。
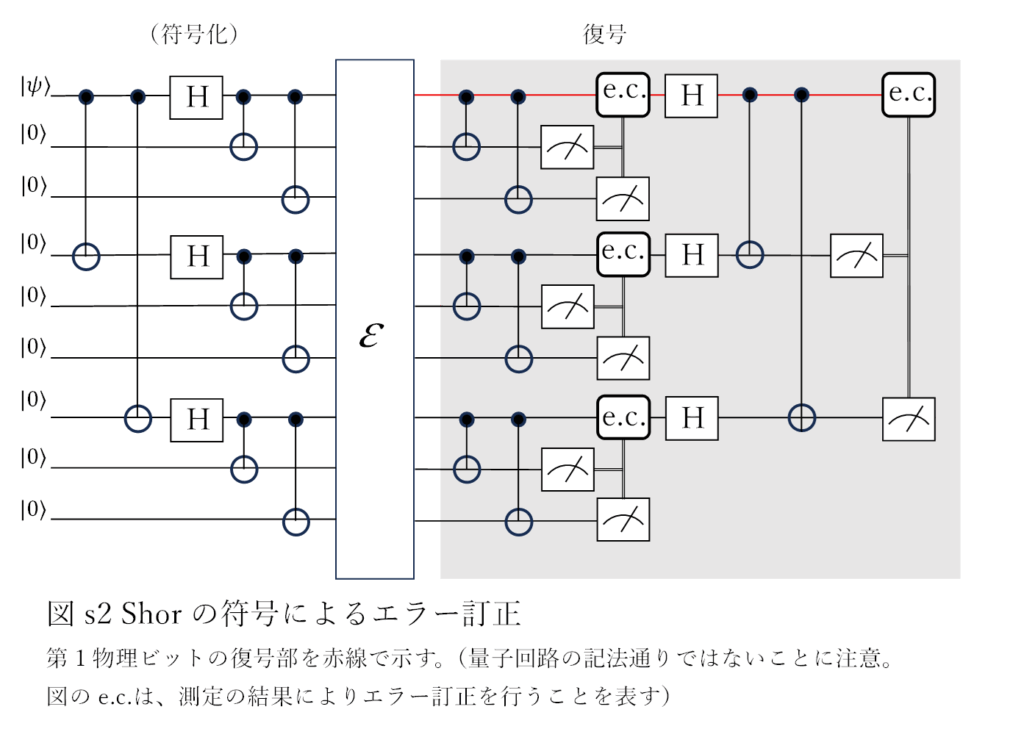
この論理ビット(たとえば\(\left|0_L\right\rangle\))の第1物理ビットに(s1)式のような変換が起こると、ある確率で第2項の\(E_1=\left[\begin{matrix}0&\sin{\theta}\\0&0\\\end{matrix}\right]\)という変換が生じて(正規化因子を省略)***、エラーが起こる前の初期状態\(\left|\psi\right\rangle\)は、\(E_1\left|\psi\right\rangle\)となる。E1はE1∝X+iY=X+iXZ=X(I+iZ)と分解することができる。この式から、まず、ビット反転(X)は確定的に起こることになる。これは、第2、第3物理ビットとの間でのCNOTによるパリティーチェック、測定(エラー判定)→ビット反転 の手順により修正する。位相反転についてはI, Zの足し合わせになっているが、第4、第7ビットとの間でのパリティーチェック、測定によりいずれかの状態に収縮するので、測定結果に応じて、必要があれば修正する****。(ビット反転、位相反転が単独で起こった場合の手順は教科書やインターネット上で説明されている。それが複合したE1のような状態に対するエラー訂正についての説明はあまり見かけないので、この例で、簡単に手順を説明した)
*Shorの符号では、論理ビットは9個の物理ビットにより、\(\left|0_L\right\rangle=\frac{1}{2\sqrt2}\left(\left|000\right\rangle+\left|111\right\rangle\right)\left(\left|000\right\rangle+\left|111\right\rangle\right)\left(\left|000\right\rangle+\left|111\right\rangle\right),\ \left|1_L\right\rangle=\frac{1}{2\sqrt2}\left(\left|000\right\rangle-\left|111\right\rangle\right)\left(\left|000\right\rangle-\left|111\right\rangle\right)\left(\left|000\right\rangle-\left|111\right\rangle\right)\) と符号化される([2] p.174)。
**通常、ある量子ビットの測定は他の量子ビットに影響を与える。たとえば、図s2の第2、第3ビットの測定では、第1ビットがI(エラーなし)、X(ビット反転)のときは第2、第3ビットのパリティーは確定しているので第1ビットには影響しない([2]のp.172)。その重ね合わせになっているときは第2、第3ビットの測定により、I, Xのどちらかに収束するので、測定結果に従ってIまたはXを演算することによってエラー訂正ができる。
***念のため:E1はrankが2でなく、そのため\(\left|\psi\right\rangle\) が\(\left|0_q\right\rangle\) 成分を含むとき、E1により、\(\left|0_q\right\rangle\) →0 と変換される。0とは、どんな状態か、\(\left|0_q\right\rangle\) 成分はどこへ消えてしまうのか、考えたくなるが… \(\left|\psi\right\rangle=\left|0_q\right\rangle\) のとき(\(1\left|0_q\right\rangle+0\left|1_q\right\rangle\) のとき)は、E1により0になってしまうように見えるが、上カッコ内のように、この場合は、第2項自体がない。それ以外の場合は、密度行列の中で第2項が選択された時には(\(\left|0_q\right\rangle\) 成分があるので)出力は必ず\(\left|0_q\right\rangle\) となり、実際の測定で、「0」に遭遇することはない。
(いろいろ疑問がわく部分ではある。が、次に進みたい。)
****オペレータE1の分解ではなく、もっと直接的にも手順を確認できる。たとえば\(\left|0_L\right\rangle\))の第1物理ビットにE1が作用すると、\(\left|0_L\right\rangle\))の一番目のカッコは(上記注***の\(\left|0\right\rangle\rightarrow0\)に変換される現象により)、\(\left(\left|000\right\rangle+\left|111\right\rangle\right)\rightarrow\left|011\right\rangle\) になる(正規化因子省略)。図s2のように第1物理ビット(図s2の赤線)を第2、第3物理ビットとパリティーチェック(CNOT)して測定することによりビット反転のエラーが確定するので、エラー訂正する。その後、(位相反転の検出のため)Hを演算すると、第4、第7物理ビットは\(\left|0\right\rangle+\left|1\right\rangle=\left|+\right\rangle\)(以下全て正規化因子省略)であることから、Hにより\(\left|0\right\rangle\)になるが、第1物理ビットは(\(\left|1\right\rangle=\left|+\right\rangle+\left|-\right\rangle\)なので)\(\left|1\right\rangle\)と\(\left|0\right\rangle\)の重ね合わせになる。同様にパリティーチェックの後、測定を行うことによりいずれかに確定するので、必要に応じてエラー訂正を行うことで、エラー訂正が完了する。
この例を見ると、量子エラーは(エラーをいう言葉から想像されるような)偶発的な、エネルギーの外場への散逸というよりも、①外場のモードとの結合による重ね合わせの発生→②測定による、ある確率でのエラーの確定(波束の収縮)の2段階で起こっている。
外界とのモードの結合を引き起こす状態変化は様々で、アナログ的だが、そのアナログ性は測定による終状態の発生確率に押し込められ、確定したエラーはデジタル的であることから、エラー訂正が可能になることがわかる。
Ekの個数に関する注: 補遺の例では、外場が\(\left|0_e\right\rangle\)の純粋状態であることから、Ekは上記の2個(\(E_0=\left\langle0_e\middle| B\middle|0_e\right\rangle\)、\(E_1=\left\langle1_e\middle| B\middle|0_e\right\rangle\))だけで表現できる。
有限温度の場合(\(\rho_{\mathrm{env}}=p\left|e_0\right\rangle\left\langle e_0\right|+\left(1-p\right)\left|e_1\right\rangle\left\langle e_1\right|\))は、\(\left\langle0_e\middle| B\middle|1_e\right\rangle\)、\(\left\langle1_e\middle| B\middle|1_e\right\rangle\)も必要になるため、「対象の系の状態変化:全系がわかっているとき」の最後に記載したとおり、d2=4個になる。(例えば、[1]の一般化振幅ダンピング(8.116~119)。このE0~E3の導出のための(外場を含めた)ユニタリ変換は[4]等に記載されている。)
2025.9.3公開