この記事の目的
量子もつれ状態 \(\frac{\left(\left|\uparrow\right\rangle\left|\downarrow\right\rangle-\left|\downarrow\right\rangle\left|\uparrow\right\rangle\right)}{\sqrt2}\) は、非常に量子論的な状態の一つだと考えられているが、この状態が決定論的には説明できず、量子論的に説明する必要があるとの共通認識が確立するためには、EPR論文による問題提起、Bellの不等式の提案、その不等式に対する多くの実験検証が必要だった。
本記事では、「隠された変数」という、シンプルな仮定からBellの不等式が導かれることを示す。この、あまり定量的に見えない仮定から、2個の粒子の測定値の相関にある定量的な制限がかかることに注目して、導出した。
作成にあたって、[1]を参考にした。Bellの不等式の導出については、[1]~[4]等多くの記事があるが、ここでは、上記の観点で導出している。
参考文献
[1]筒井 ベル不等式:その物理的意義と近年の展開 日本物理学会誌 Vol. 69, No. 12, 2014 69-12_836.pdf
[2]三浦 局所実在論とBellの不等式 quantph_bellinequality.pdf
[3]Matsumoto CHSH不等式の解説 qph-article04.pdf
[4]EMAN CHSH不等式 https://eman-physics.net/quantum/chsh.html
[5] A. Einstein, B. Podolsky and N. Rosen: Phys. Rev. 47 (1935) 777.
[6] J. S. Bell: Physics 1 (1964) 195.
[7] J. F. Clauser, M. A. Horne, A. Shimony and R. A. Holt: Phys. Rev. Lett. 23
(1969) 880.
背景
量子もつれ状態は、(因果律に従う、決定論的な)マクロな世界に生きている人間(私を含めた)にはわかりにくい、不思議な状態だが、量子コンピュータでは、2ゲート演算を行うとすぐに表れる。エラー耐性を高めるために量子もつれが作られ、エラー検出のためには、もつれていた量子ビットのもつれをほどいたりもする。量子コンピュータ独特の技術は、量子もつれを使った操作から生まれる。
しかし、量子コンピュータにおいて、①隣り合った量子ビットに相互作用を与え、2量子ビット演算により量子もつれ状態にする。(たとえば、\(\left|\uparrow\right\rangle\left|\downarrow\right\rangle-\left|\downarrow\right\rangle\left|\uparrow\right\rangle\)(正規化因子を略す))②相互作用をとめる。2個の量子ビットは独立になる。③一方の量子ビットを測定する。↑なら、他方は(相互作用はとめたのに)自動的に↓になっている。というのはどういうことなのか?相互作用はとめて、お互いは独立になっているはず…
なかなか、のみこみづらいと感じる。
量子もつれ状態の存在自体は、実験的に確認されているので、その存在は、のみこむしかない(力学をするときに、万有引力の存在をのみこむしかないように)。
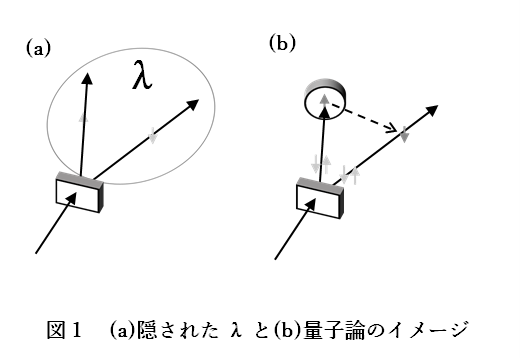
よくある例では、(パラメトリック下方変換等で)同時に生成された、2個の2準位系の粒子(光子等)は、生成された瞬間から別の方向に飛んでいく。十分に離れて、お互いに相互作用がないと考えられる時点で一方を測定する。その結果が↑(またはV偏光)であれば、他方が↓(またはH偏光)であることが確定する。逆に↓であれば他方は↑となる。最初に測定する粒子が↑か↓か、は確定していない。測定された瞬間に確率的に定まると(量子論では)説明される(図1(b))。量子コンピュータの、上記の現象と同じものになる。
マクロな世界では聞き慣れない考え方で、実際アインシュタインは、もっとわかりやすい決定論的な理論=隠されたパラメータの理論 があるはずと考えた(EPR論文[5]は、その立場から量子論に対する意見を提示したもの)。Bellは、隠されたパラメータの理論と量子論では、量子もつれ状態について測定される結果に違いが現れることを示し(Bellの不等式)[6]、その後の多くの実験により、量子論の方に軍配が上がる結果になった。
その結果、マクロな世界に住む人間は量子もつれ状態と、その量子論的な説明を、その通りのみこむしかなくなった。
この記事では、Bellの不等式の導出を中心に、このストーリーをまとめる。
決定論的な理論=隠れたパラメータの理論 からベルの不等式へ
量子論的な説明でわかりにくいのは、2個の粒子が生成された時点では、↑か↓かは不明で、その後の、お互いの距離がずっと遠くなってしまったどこかの時点で一方を測定すると、その瞬間に他方のスピンが確定するというところになる。
しかし、実は生成された時点でどちらかにスピンが決まっている、ということなら、それほど妙なことではない。同じ場所にいる、できたばかりの2個の粒子が相互作用することでお互いの状態が確定した、ただ、人間にはその相互作用の様子を完全に見ることができないので、測定してみるまでわからなかっただけだ、と考えられる。そうすると、ケース①:粒子1が↑、粒子2が↓、ケース②:粒子1が↓、粒子2が↑が、ある規則(生成時の相互作用の具合)によって現れるということになる。この①、②が隠れた変数になる。
もちろん、粒子1、2はz軸方向に測定するとは限らず、x, yまたはその中間的な方向で測定するかもしれない。1、2で別の軸で測定を行うかもしれない。その全てについて答えを用意しておかなければならない。そこで、隠れた変数は①、②の2個だけではなく、連続量、複数次元になるかもしれないが、生成された時点で状態が決まるということになり、(慣れ親しんだ決定論なので)わかりやすい。
Bellの不等式は、理論の具体的な内容には触れず、隠れた変数があることだけを仮定したときに導き出される、測定値の間に現れる不等式になる。量子論的な説明では、この不等式を満たさない場合があるため、実験的に量子論、隠れた変数の理論のどちらが正しいかを判定できる。
実際の測定は、多数回の同じ測定を平均することで行われるため、隠れた変数の理論でも、複数回の測定による期待値は計算可能である必要がある。隠れた変数をλとすれば(λは離散変数、連続変数、多変数であってもよい)、期待値は、
$$E\left(A\right)=\int{d\lambda\ \rho\left(\lambda\right)}A\left(\lambda\right)$$
と表すことができる。(ρ(λ)はλが現れる頻度を表す分布関数。一定の条件で測定を繰り返した場合の測定値の期待値は、ある分散の中で一定値になることから、ある時間、またはある回数の測定の中で、定まった頻度でλが現れるとしている。)
図1のように、ある時点で発生した、2準位系のA, B2個の粒子に対して、a, b軸で測定を行った結果の相関をとる。式としては、
$$C\left(\boldsymbol{a},\boldsymbol{b}\right)=\int{d\lambda\ \rho\left(\lambda\right)}A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)$$
個々の測定結果は(2準位系なので)↑、↓や、HとV等の2値になるが、ここでは±1とする。すると、本式の \(A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)\) は、双方が1または-1のときに1、逆符号のときに-1となり、確かに相関(逆相関)を表している。その測定を何回も繰り返した時の平均値が \(C\left(\boldsymbol{a},\boldsymbol{b}\right)\) になる。
最もシンプルな実験として、2個の粒子を同じz軸で測定することが考えられるが、この実験では100%の逆相関が得られる。そこで、隠れた変数の理論でも、\(A\left(\boldsymbol{a},\lambda\right)=-B\left(\boldsymbol{a},\lambda\right)\)を仮定する。
複数の測定軸での実験では、測定結果はそれほど明らかではなく、この場合についての考察により、オリジナルのBellの不等式、CHSH型[7]の不等式が得られた。
実験検証に通常使われるのはCHSH型の不等式で、下記のように表される。
\(\left|C\left(\boldsymbol{a},\boldsymbol{b}\right)+C\left(\boldsymbol{a},\boldsymbol{b}’\right)+C\left(\boldsymbol{a}’,\boldsymbol{b}\right)-C\left(\boldsymbol{a}’,\boldsymbol{b}’\right)\right|\le2\) (A)
実験的には、Aに対してa軸、a’軸の測定、それと同じタイミングで、Bに対してb軸、b’軸の測定を行い、合計4種類の測定を多数回行うことにより、左辺が得られる。
上式により積分形にすれば、
$$\left|\int{d\lambda\ \rho\left(\lambda\right)}\left\{A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)+A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)+A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b},\lambda\right)-A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)\right\}\right|\le2$$
被積分関数の中の \(\left\{A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)+\cdots-A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)\right\}\) のそれぞれの項は、異なる軸に対する、異なる時間の1回の測定結果になるが、λが決まれば確定した値になる。λが、別の軸での測定のときも常に同じ頻度ρ(λ)で現れることから、同じλをもつ測定を集めて足し合わせることができる。実は、どのλに対しても、
\(\left|A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)+\cdots-A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)\right|\le2\) (B)
が成立し、(A)が成り立つこと。以下で説明する。(以下、通常の導出よりいくらか長くなるが、隠されたλの仮定から、測定される相関に制限が現れるという観点から説明する。)
被積分関数は、\(A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)+A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)+A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b},\lambda\right)\)と、\(A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)\)の差になっていて、それぞれの項はA, Bの測定値の相関の正負に応じて±1になっている。すぐわかるように、この差は4以下で、かつ偶数になる。全ての物理量は(ρに応じて)任意の±1を取ることができるので、上記の各項(A, Bの測定値の相関)も任意の±1を取ることができるように感じるが、実は制限があり、そのため、4, -4をとれない(つまり絶対値で2以下)ことが、以下のようにしてわかる。
この差が4になるのは、\(\left(A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right),A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b}’,\lambda\right),A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b},\lambda\right),A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)\right)=\left(1,1,1,-1\right)\)のとき、-4になるのは(-1,-1,-1,1)になるときに限られるが、
- 最初の3項が1,1,1の場合:\(A\left(\boldsymbol{a},\lambda\right),B\left(\boldsymbol{b},\lambda\right)\)及び、\(A\left(\boldsymbol{a},\lambda\right),B\left(\boldsymbol{b}’,\lambda\right)\)及び、\(A\left(\boldsymbol{a}’,\lambda\right),B\left(\boldsymbol{b},\lambda\right)\)が正の相関をもつ(同じ符号である)ということになる。順序を変えると、\(A\left(\boldsymbol{a}’,\lambda\right)\Leftrightarrow B\left(\boldsymbol{b},\lambda\right),\ \ B\left(\boldsymbol{b},\lambda\right)\Leftrightarrow A\left(\boldsymbol{a},\lambda\right),\ \ A\left(\boldsymbol{a},\lambda\right)\Leftrightarrow B\left(\boldsymbol{b}’,\lambda\right) \) が正の相関を持つ。つまり、\(A\left(\boldsymbol{a}’,\lambda\right)\Leftrightarrow B\left(\boldsymbol{b},\lambda\right)\Leftrightarrow A\left(\boldsymbol{a},\lambda\right)\Leftrightarrow B\left(\boldsymbol{b}’,\lambda\right)\) が正の相関を持つ(隣り合う2個の値が同符号)。すると、両端の\(A\left(\boldsymbol{a}’,\lambda\right),B\left(\boldsymbol{b}’,\lambda\right)\) も正の相関を持つことになる(\(A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)=1\) )。従って、(1,1,1,-1)になることはできない。
- -1,-1,-1の場合:\(A\left(\boldsymbol{a}’,\lambda\right)\Leftrightarrow B\left(\boldsymbol{b},\lambda\right)\Leftrightarrow A\left(\boldsymbol{a},\lambda\right)\Leftrightarrow B\left(\boldsymbol{b}’,\lambda\right)\) が全て負の相関になる(矢印の左右の値の符号が逆)。そうすると \(A\left(\boldsymbol{a}’,\lambda\right),B\left(\boldsymbol{b}’,\lambda\right)\) は(3回符号が逆転するので)負の相関を持つ( \(A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)=-1\) )。従って、(-1,-1,-1,1)になることはできない。
上記 1., 2.より、全てのλについて、(B)が成立する。これにρ(λ)をかけて積分した
$$\int{d\lambda\ \rho\left(\lambda\right)}\left|A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b},\lambda\right)+A\left(\boldsymbol{a},\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)+A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b},\lambda\right)-A\left(\boldsymbol{a}’,\lambda\right)B\left(\boldsymbol{b}’,\lambda\right)\right|\le2$$
が成立するため、絶対値符号を外に出した(A)も、成立する(三角不等式)。
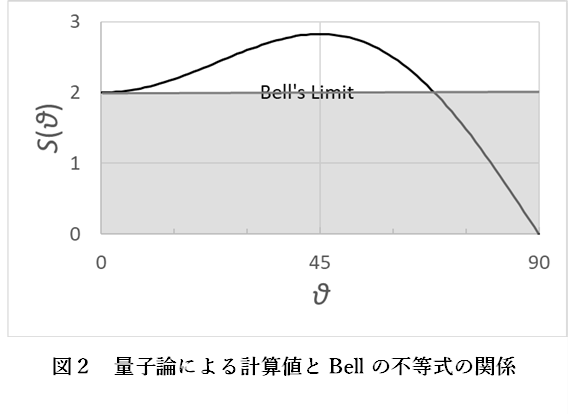
一方、量子論的な計算では、たとえば \(\theta_{ab}=\theta_{ab’}=\theta_{a’b}=\theta\)、\(\theta_{a’b’}=3\theta\) のとき、(A)の左辺をS(θ)とすれば、
$$S\left(\theta\right)=\left|3\cos{\theta}-\cos{3\theta}\right|$$
となる[1]。すると、θ=π/4等、広い範囲で2より大きい値になり、量子論と決定論との間に差が出ることがわかる(図2)。この違いについては、多くの「抜け穴」をふさぎながら高精度の実験が行われ、(マクロな世界に住む人間には残念なことに)量子論による計算が、実験を非常によく再現することが明らかになった。[1]
これにより、人間は常に世界が決定論的に動くとは限らないことを、のみこまざるを得なくなった。(個人的には、λのある世界にいると思っていた方が落ち着けた…)
CHSH型不等式の導出についての追記
隠れた変数の理論では、理論の具体的な形には触れないので、λ毎に定まる測定値 \(A\left(\boldsymbol{x},\lambda\right),B\left(\boldsymbol{y},\lambda\right)\) に対する制限はつけられないが、A, Bの測定値の相関(掛け算)については、測定方向を循環的に設定することで、1., 2.のように関係性が現れる。相関の積分値 \(C\left(\boldsymbol{x},\boldsymbol{y}\right)\) のように、λでの相関を \(C_\lambda\left(\boldsymbol{x},\boldsymbol{y}\right)=A\left(\boldsymbol{x},\lambda\right)B\left(\boldsymbol{y},\lambda\right)\) と書けば、1., 2.の関係性は \(C_\lambda\left(\boldsymbol{a}’,\boldsymbol{b}’\right)=C_\lambda\left(\boldsymbol{a},\boldsymbol{b}\right)C_\lambda\left(\boldsymbol{a},\boldsymbol{b}’\right)C_\lambda\left(\boldsymbol{a}’,\boldsymbol{b}\right)\) と書ける。(∵ \(C_\lambda\left(\boldsymbol{a},\boldsymbol{b}\right)C_\lambda\left(\boldsymbol{a},\boldsymbol{b}’\right)C_\lambda\left(\boldsymbol{a}’,\boldsymbol{b}\right)=C_\lambda\left(\boldsymbol{a}’,\boldsymbol{b}\right)C_\lambda\left(\boldsymbol{a},\boldsymbol{b}\right)C_\lambda\left(\boldsymbol{a},\boldsymbol{b}’\right)=A\left(\boldsymbol{a}’,\lambda\right)\left\{B\left(\boldsymbol{b},\lambda\right)\right\}^2\left\{A\left(\boldsymbol{a},\lambda\right)\right\}^2B\left(\boldsymbol{b}’,\lambda\right)\) 1., 2.以外の場合にも成り立つ)
EPRの論文以来30年手つかずになっていた(ように見える)問題について、隠れたλがあるという、あまり定量的ではない仮定だけで、このような関係式を導き、量子論との測定結果の違いを不等式として定量化した*、Bellの業績は、(言わずもがなだが、)すごいことだと感じる。
*オリジナルの不等式の導出は、「補足」に、記載した。こちらも、測定値の「相関」には制限が出る、という要件から導出できる。
補足:オリジナルの不等式の導出
Bellが導いたオリジナルの不等式は下記のようになる。これも、同じ考え方で導出できることを示す。
\(\left|C\left(\boldsymbol{a},\boldsymbol{b}\right)-C\left(\boldsymbol{a},\boldsymbol{c}\right)\right|\le1+C\left(\boldsymbol{b},\boldsymbol{c}\right)\) (C)
同じように、同じλ同士で、左辺、右辺を比較する。
左辺= \(\left|C_\lambda\left(\boldsymbol{a},\boldsymbol{b}\right)-C_\lambda\left(\boldsymbol{a},\boldsymbol{c}\right)\right|\) (λ毎の絶対値について比較する)
右辺= \(1+C_\lambda\left(\boldsymbol{b},\boldsymbol{c}\right)\)
この導出では、同じ軸xで測定する場合、追加で \(A\left(\boldsymbol{x},\lambda\right)=-B\left(\boldsymbol{x},\lambda\right)\) であることを使う。
左辺がともに正の相関、または逆の相関のとき、左辺は0。この時、b軸とc軸の測定値については、「追記」の議論と同様にすると、 \(C_\lambda\left(\boldsymbol{a},\boldsymbol{b}\right)C_\lambda\left(\boldsymbol{a},\boldsymbol{c}\right)=B\left(\boldsymbol{b},\lambda\right)\left\{A\left(\boldsymbol{a},\lambda\right)\right\}^2B\left(\boldsymbol{c},\lambda\right)=B\left(\boldsymbol{b},\lambda\right)B\left(\boldsymbol{c},\lambda\right)\) であることから、 \(B\left(\boldsymbol{b},\lambda\right),B\left(\boldsymbol{c},\lambda\right)\) は正の相関になる。\(A\left(\boldsymbol{b},\lambda\right)=-B\left(\boldsymbol{b},\lambda\right)\) であることを利用すると、 \(C_\lambda\left(\boldsymbol{b},\boldsymbol{c}\right)=-1\) なので、右辺は0。(測定方向はやはり循環的に設定されているが、3個の測定のため、3個目の相関を他の2個の相関の結果から導く際に、Bの測定値を、同じ軸のAの測定値に変換する手順が必要になった)
一方、左辺の一方が正の相関、他方が逆相関のとき、左辺は2。 \(B\left(\boldsymbol{b},\lambda\right),B\left(\boldsymbol{c},\lambda\right)\) は負の相関になることと、\(A\left(\boldsymbol{b},\lambda\right)=-B\left(\boldsymbol{b},\lambda\right)\) を利用すると、右辺は2。
従って、いずれの場合も左辺=右辺となる。CHSHのときと同様に、ρ(λ)をかけて積分し、三角不等式を利用することで、(C)が導出される。
CHSH不等式が、 \(A\left(\boldsymbol{a}’,\lambda\right),B\left(\boldsymbol{b}’,\lambda\right)\) の相関が定まることから導出されたように、 \(A\left(\boldsymbol{b},\lambda\right),B\left(\boldsymbol{c},\lambda\right)\) の相関が定まるために、(C)が成り立つ。
(「隠れたρ」によって、測定値には特に制限が出ないが、「相関」については制限が現れ、その結果、相関の間に、ある関係が現れることが見やすい導出になっている。また、オリジナル、CHSH型の不等式を同じ考え方で導出することにもなっている。)
2025.3.28公開