本記事の目的
量子コンピューティングは、通常のコンピュータと全く違う計算方法が使われることにより高速化される。しかし、その計算方法は全てのアルゴリズムに適用可能なわけではない。
量子コンピューティングで対数関数的な計算時間の短縮が可能な理由について、フーリエ変換を例として記す。この高速化はフーリエ変換特有のアルゴリズムによって成立している。
量子フーリエ変換(QFT)のアルゴリズムは1 2等で説明されている。そこでの説明は非常にシンプルだが、通常のコンピュータのアルゴリズムとの対応関係がなく、高速化の原因がわかりにくい。本記事では、通常のコンピュータのアルゴリズムであるFFTと対応させて説明することで、QFTの高速化の原因を明らかにする。
量子コンピュータの基本的なアイデア
量子コンピュータの基本的なアイデアは、下記のようになる。
- n個の2準位の量子ビットを基底とする。
- このnビットの量子システムに対して、量子力学的に実現可能なユニタリ変換により、計算を行う。
もう少し詳しく書くと、
- データは、n個の2準位の量子ビットに、通常のコンピュータのように \(|0\rangle\), \(|1\rangle\) の2値でデータを入れるのではない。
量子コンピュータでは、個々の量子ビットに \(a|0\rangle+b|1\rangle\) の形で(アナログ、または多ビットの)データを入れることにより、1ビットあたりのデータ量を増やすことができるが、それだけでは量子コンピュータに特徴的な量子計算はできない。
n 量子ビットの直積の \(\left|j_0\right\rangle\left|j_1\right\rangle\ldots\left|j_{n-1}\right\rangle\) の線形結合の係数にデータを格納することにより、n qubitで2nの(アナログ、または多ビットの)データを格納できる。また、次項以降で説明する特徴的な計算が可能になる。
直積の線形結合は上記の \(a|0\rangle+b|1\rangle\) の直積とは異なり、量子もつれ状態になっている。量子もつれ状態へのデータ入力により、nビットデータへの2nデータの入力が可能になり、また高速の処理が可能になる。
(n=3の場合、23=8 qubit( \(\left|000\right\rangle,\left|001\right\rangle,\left|010\right\rangle,\left|011\right\rangle,\left|100\right\rangle,\left|101\right\rangle,\left|110\right\rangle,\left|111\right\rangle\) )の線形結合の係数にデータを入れられる。) - 量子計算は、直積になっているn量子ビットのうち、i番目の量子ビットをユニタリ変換する、またはi番目とj番目の量子ビットをユニタリ変換することで行われる。i番目の量子ビット、またはi番目とj番目の量子ビットを持つ全ての直積上のデータを一斉に変換することができるので、高速な処理が可能になる。
しかし、当然ながら、このような全データに対する一律な処理が含まれるアルゴリズムは限られているので、量子コンピュータは、そのようなアルゴリズムに限って、非常に高速な処理が可能な計算機ということになる。
*この1.2.に関しては、本記事末尾の「「基本的なアイデア」に関する追記」でさらに詳述した。
量子コンピュータは、上記のように、ごく限られたアルゴリズムしか高速化できない。ただし、その中にはフーリエ変換、固有値計算等、有用で、かつ通常のコンピュータでは計算能力が不足するものが含まれているため、開発が進められている。3
たとえばフーリエ変換はRSA暗号の安全性に関わる素因数分解問題の中で最も時間のかかるプロセスで、また、量子化学計算等、フーリエ変換の速度がボトルネックとなる、応用的に重要なアルゴリズムも複数ある。
フーリエ変換の高速化の仕組み
通常のコンピュータでの高速化(高速フーリエ変換 FFT)
N個のデータに対する離散フーリエ変換は
$$ X_j=\sum_{k=0}^{N-1}{x_ke^{\frac{i2\pi jk}{N}}}$$ と表すことができる。行列で表すこともでき、
$$\left[\begin{matrix}\\X_j\\\\\end{matrix}\right]=\left[\begin{matrix}&&\\&e^{\frac{i2\pi jk}{N}}&\\&&\\\end{matrix}\right]\left[\begin{matrix}\\x_k\\\\\end{matrix}\right]$$行列の要素数分の計算が必要になるので、N2回(N=2nなら (2n)2回)の計算が必要になる。
離散フーリエ変換の通常のコンピュータでの計算アルゴリズムとして、高速フーリエ変換(FFT)が知られている4。
FFTでは、\(X_j\)のそれぞれについて、N=2nのとき、nステップの計算ですむため、計算回数を大幅に削減することができる( (2n)2回→n 2n回 )。
量子フーリエ変換(QFT)との比較をするため、N=8=23の場合の計算手順を上記参考文献に従って確認する。
\(\left[\begin{matrix}\begin{matrix}X_0\\X_1\\X_2\\\end{matrix}\\\vdots\\X_7\\\end{matrix}\right]=\left[\begin{matrix}\begin{matrix}1&1&1\\1&W_8^\ &W_8^{\ 2}\\1&W_8^{\ 2}&W_8^4\\\end{matrix}&\cdots&\begin{matrix}1\\W_8^{\ 7}\\W_8^{14}\\\end{matrix}\\\vdots&\ddots&\vdots\\\begin{matrix}1&W_8^{\ 7}&W_8^{14}\\\end{matrix}&\cdots&W_8^{49}\\\end{matrix}\right]\left[\begin{matrix}\begin{matrix}x_0\\x_1\\x_2\\\end{matrix}\\\vdots\\x_7\\\end{matrix}\right]\) ただし、\(W_m=e^\frac{i2\pi}{m}\)
\(W_8^4=-1\) 等を利用すると、下記のようになる。( \(X_n\) はビットリバース順(2進数の桁を逆転)。次の式を導出する都合で、\(W_8^5\) 等も一部残っている。)
\(\begin{eqnarray}X_0&=&x_0+x_1+x_2+x_3+x_4+x_5+x_6+x_7\\
X_4&=&x_0-x_1+x_2-x_3+x_4-x_5+x_6-x_7\\
X_2&=&x_0+x_1W_8^{\ 2}-x_2-x_3W_8^{\ 2}+x_4+x_5W_8^{\ 2}-x_6-x_7W_8^{\ 2}\\
X_6&=&x_0-x_1W_8^{\ 2}-x_2+x_3W_8^{\ 2}+x_4-x_5W_8^{\ 2}-x_6+x_7W_8^{\ 2}\\
X_1&=&x_0+x_1W_8^\ +x_2W_8^{\ 2}+x_3W_8^{\ 3}-x_4-x_5W_8^\ -x_6W_8^{\ 2}-x_7W_8^{\ 3}\\
X_5&=&x_0-x_1W_8^\ +x_2W_8^{\ 2}-x_3W_8^{\ 3}-x_4+x_5W_8^\ -x_6W_8^{\ 2}+x_7W_8^{\ 3}\\
X_3&=&x_0+x_1W_8^3-x_2W_8^{\ 2}-x_3W_8^5-x_4-x_5W_8^{\ 3}+x_6W_8^{\ 2}+x_7W_8^{\ 5}\\
X_7&=&x_0-x_1W_8^3-x_2W_8^{\ 2}+x_3W_8^5-x_4+x_5W_8^{\ 3}+x_6W_8^{\ 2}-x_7W_8^{\ 5}\end{eqnarray}\)
\(x_n\)もビットリバース順に整理すると、規則性があることがわかる。
\(\begin{eqnarray}X_0&=&\left\{\left(x_0+x_4\right)+\left(x_2+x_6\right)\right\}+\left\{\left(x_1+x_5\right)+\left(x_3+x_7\right)\right\}\\
X_4&=&\left\{\left(x_0+x_4\right)+\left(x_2+x_6\right)\right\}-\left\{\left(x_1+x_5\right)+\left(x_3+x_7\right)\right\}\\
X_2&=&W_4^{\ 0}\left\{\left(x_0+x_4\right)-\left(x_2+x_6\right)\right\}+W_4^{\ 1}\left\{\left(x_1+x_5\right)-\left(x_3+x_7\right)\right\}\\
X_6&=&W_4^{\ 0}\left\{\left(x_0+x_4\right)-\left(x_2+x_6\right)\right\}-W_4^{\ 1}\left\{\left(x_1+x_5\right)-\left(x_3+x_7\right)\right\}\\
X_1&=&\left\{W_8^{\ 0}\left(x_0-x_4\right)+W_8^{\ 2}\left(x_2-x_6\right)\right\}+\left\{W_8^{\ 1}\left(x_1-x_5\right)+W_8^{\ 3}\left(x_3-x_7\right)\right\}\\
X_5&=&\left\{W_8^{\ 0}\left(x_0-x_4\right)+W_8^{\ 2}\left(x_2-x_6\right)\right\}-\left\{W_8^{\ 1}\left(x_1-x_5\right)+W_8^{\ 3}\left(x_3-x_7\right)\right\}\\
X_3&=&W_4^{\ 0}\left\{W_8^{\ 0}\left(x_0-x_4\right)-W_8^{\ 2}\left(x_2-x_6\right)\right\}+W_4^{\ 1}\left\{W_8^{\ 1}\left(x_1-x_5\right)-W_8^{\ 3}\left(x_3-x_7\right)\right\}\\
X_7&=&W_4^{\ 0}\left\{W_8^{\ 0}\left(x_0-x_4\right)-W_8^{\ 2}\left(x_2-x_6\right)\right\}-W_4^{\ 1}\left\{W_8^{\ 1}\left(x_1-x_5\right)-W_8^{\ 3}\left(x_3-x_7\right)\right\}\end{eqnarray}\)
この式を、下記の規則でダイアグラムにすると、量子計算との対応がわかりやすい。
\(\left[\begin{matrix}a\\b\\\end{matrix}\right]\rightarrow\left[\begin{matrix}a+b\\W_m^n\left(a-b\right)\\\end{matrix}\right]\) の変換を

と書く(バタフライ演算)ことにすると、上式は、

のようなダイアグラムで書き表すことができる。
このバタフライ演算により、左から右に向かう演算は、3ステップで終了している。本来個々の\(X_j\)を求めるためには、全ての\(x_j\)に係数をかけて足し算をする、23ステップの計算が必要だったので、ステップ数が対数関数的に減少したことになる。
しかし、縦方向のバタフライ演算は全てのステップで23回必要になり、縦方向の計算回数はFFTでは減らすことができない。そこで、FFTは横方向の計算量は対数関数的に減少させられるものの、縦方向については減少させられず、トータルとして計算量の対数関数的な減少は達成できないという問題がある。
量子フーリエ変換(QFT)の高速化
しかし、このダイアグラムを見ると、このバタフライ演算は非常に量子演算と親和性が高いことがわかる。\(x_0{{,x}_1,\ldots,x}_7\) のデータが3個の量子ビットの直積 \(\left|000\right\rangle,\left|001\right\rangle,\ldots,\left|111\right\rangle\) の係数にコーディングされている場合、第1ステップは最上位量子ビット(第1量子ビット)の \(\left|0\right\rangle,\left|1\right\rangle\) 間でのバタフライ演算(例えば、\(x_0,x_4\) は \(\left|000\right\rangle,\left|100\right\rangle\) という、第1量子ビットだけが異なる組み合わせになっている)、第2ステップは第2量子ビット、第3ステップは第3量子ビットでのバタフライ演算になっている。(本稿末尾の「「基本的なアイデア」に関する追記 2.について」 に記載した、n=3の場合のHの変換行列を見ると、このバタフライ演算との類似性がわかる)
量子演算で、2個の要素の足し算と引き算を出力する操作はH変換になるが、たとえば第1ビットに対するHのようなユニタリ変換をすると、\(\left|000\right\rangle,\left|001\right\rangle,\ldots,\left|111\right\rangle\) の全てが一度にHの変換を受ける(それぞれの第1量子ビットが1回の量子演算で全て \(\left[\begin{matrix}\left|0\right\rangle\\\left|1\right\rangle\\\end{matrix}\right]\rightarrow\frac{1}{\sqrt2}\left[\begin{matrix}\left|0\right\rangle+\left|1\right\rangle\\\left|0\right\rangle-\left|1\right\rangle\\\end{matrix}\right]\) に変換される)。つまり、上図の第1ステップの4個のバタフライ演算が、1回のH変換、(及び、後述する、その他のビットをコントロールビットとした2回の位相回転ゲート)で完了してしまう。そこで、FFTで達成できなかった、縦方向の計算量の減少、その結果、トータルの計算量の対数関数的な減少が達成できることになる。
*同時に、この例から、量子計算での高速化は、アルゴリズムの特殊な規則性(2n個のデータの変換が、n個の、ビットごとにまとめた変換で達成できる)により達成されていることがわかる。従って量子コンピュータはあらゆるアルゴリズムに対して有用なものではないことに注意する必要がある。
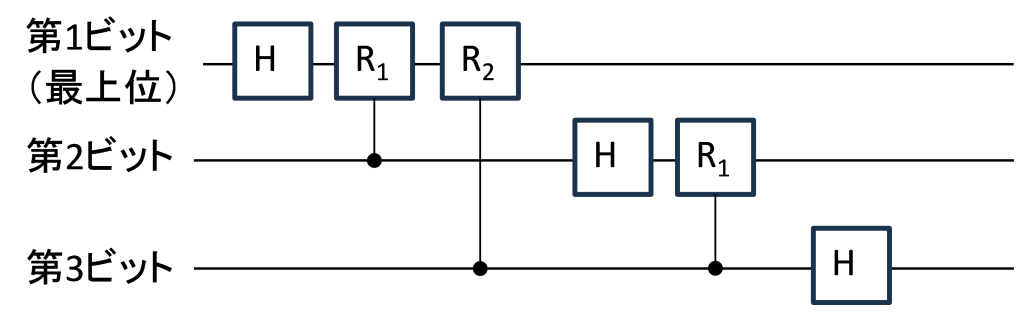
以上のことを量子回路で書くと、縦方向の計算回数が減ることがとてもわかりやすい。
\(x_0{{,x}_1,\ldots,x}_7\) のデータが \(\left|000\right\rangle,\left|001\right\rangle,\ldots,\left|111\right\rangle\) にコーディングされている場合、第1ステップのバタフライ演算は第1量子ビットの、H演算と位相回転ゲート \(\left[\begin{matrix}1&\ \\\ &e^{i2\pi p}\\\end{matrix}\right]\) の積で表される。回転量は、他のqubitの状態によって変わる(第2量子ビットが1なら \(p=\frac{1}{8}\) 、第3量子ビットが1なら \(p=\frac{1}{4}\) 、両方が1なら、その和 \(p=\frac{3}{8}\) )。そこで、他の量子ビットの状態により回転演算を行うかどうかが変わる、制御Rk(補遺 参照)を使うと、1ステップの量子計算は、下記のようになる。(\(R_k=\left[\begin{matrix}1&\ \\\ &e^\frac{i2\pi}{2^{k+1}}\\\end{matrix}\right]\) とする)
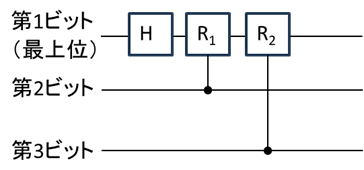
同じことを第2、第3ビットについても行うと、
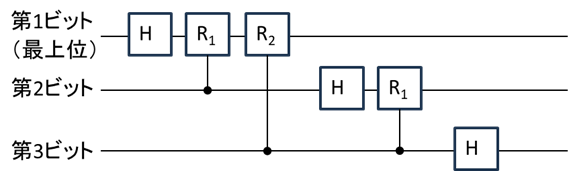
と書くことができる。回路中の□が1個の演算になるので(正確には、制御 Rkはいくつかの演算に分かれるので、□1個が1個の演算ステップになる。下記の「2量子ビット演算等に関する補遺」参照)、演算回数が非常に少なくなることが視覚的にもわかる。少なくなった原因は、2n回必要だったバタフライ演算が、HとR1, R2のように、n回ですんだことによるので、対数関数的に計算速度が高速化することになる。
「基本的なアイデア」に関する追記
- について
直積の線形結合の係数にデータを載せるという考え方に対する補足:
n=2のとき、たとえば、第1ビットと第2ビットに0, 1が現れる確率が全て(独立に)0.5である状態は、\(\left(\left|0\right\rangle+\left|1\right\rangle\right)\left(\left|0\right\rangle+\left|1\right\rangle\right)\) とかける。(正規化因子を略す)
これは、\(\left|00\right\rangle+\left|01\right\rangle+\left|10\right\rangle+\left|11\right\rangle\) と、直積の形で書くことができる。この状態は、(1,1,1,1)というデータを載せていると考えられる。
これは、直積で書き下してはあるが、元の式のように各ビットで因数分解でき(ビットごとの線形結合の直積として書くことができ)、第1ビットの状態( \(\left|0\right\rangle\) 、\(\left|1\right\rangle\) の確率)と第2ビットの状態はお互いに独立である。しかし、容易に想像できるように、直積の線形結合で書ける状態の全てが各ビットで因数分解できるわけではない。
その一例が、\(\left|00\right\rangle+\left|11\right\rangle\) のような、量子もつれ状態である。この状態は、第1ビットが\(\left|1\right\rangle\)のときは、第2ビットは必ず\(\left|1\right\rangle\)という、(別の場所にあるので)お互いに独立なはずの2個のビットの状態が他のビットによって確定する、非常に量子力学的な状態になる。量子もつれ状態は実際に作り出すことができることがわかっている5。この、量子もつれ状態まで含めると、直積の任意の線形結合の状態は作り出すことができるはずなので、その係数として、n量子ビットの系に2nのデータを入れることができるという考え方である。 - について
直積の線形結合という状態に対する量子演算についての補足:
元々の量子ビット内での演算は、量子ビット内の状態 \(a\left|0\right\rangle+b\left|1\right\rangle\) をブロッホ球上の座標で表し、その座標のx, y, z軸等での回転として定義されていた。しかし、本追記の「1.について」のような、量子もつれ状態まで含む直積の線形結合の空間では、各ビットの状態は \(a\left|0\right\rangle+b\left|1\right\rangle\) のようなシンプルな状態ではない。*
このような状態に対しても、1個の量子ビットに対して演算をするという操作(たとえば量子ビットに対するπパルスの印加)は可能である。この操作は、量子ビット内の状態 \(a\left|0\right\rangle+b\left|1\right\rangle\) のある軸に対するシンプルな描像でイメージすることができなくなる。しかし、それがたとえば第3量子ビットに対するH演算であれば、(第3量子ビットが \(a\left|0\right\rangle+b\left|1\right\rangle\) で表される場合と同様に、)変換規則 \(\left[\begin{matrix}\left|0\right\rangle_3\\\left|1\right\rangle_3\\\end{matrix}\right]\rightarrow\left[\begin{matrix}\left|0\right\rangle_3+\left|1\right\rangle_3\\\left|0\right\rangle_3-\left|1\right\rangle_3\\\end{matrix}\right]\) (正規化因子を略す)を持つ演算になるはずである。この規則ならば、直積の線形結合で表される状態に対しても適用することができる。そこで、データが3量子ビットの系に
$$a_0\left|000\right\rangle+a_1\left|001\right\rangle+a_2\left|010\right\rangle+a_3\left|011\right\rangle+a_4\left|100\right\rangle+a_5\left|101\right\rangle+a_6\left|110\right\rangle+a_7\left|111\right\rangle$$と埋め込まれているとする。第3量子ビットへのアダマールゲート(H)は、 \(\left[\begin{matrix}\left|0\right\rangle_3\\\left|1\right\rangle_3\\\end{matrix}\right]\rightarrow\left[\begin{matrix}\left|0\right\rangle_3+\left|1\right\rangle_3\\\left|0\right\rangle_3-\left|1\right\rangle_3\\\end{matrix}\right]\) なので、たとえば上式第1項は、\(a_0\left|000\right\rangle\rightarrow a_0\left(\left|000\right\rangle+\left|001\right\rangle\right)\)となる。同じことを全ての項について行うと、この8次元のデータに対する変換行列は
$$\left[\begin{matrix}1&1&\ &\ &\ &\ &\ &\ \\1&-1&\ &\ &\ &\ &\ &\ \\\ &\ &1&1&\ &\ &\ &\ \\\ &\ &1&-1&\ &\ &\ &\ \\\ &\ &\ &\ &1&1&\ &\ \\\ &\ &\ &\ &1&-1&\ &\ \\\ &\ &\ &\ &\ &\ &1&1\\\ &\ &\ &\ &\ &\ &1&-1\\\end{matrix}\right]\left[\begin{matrix}a_0\\a_1\\\begin{matrix}a_2\\a_3\\\begin{matrix}a_4\\a_5\\\begin{matrix}a_6\\a_7\\\end{matrix}\\\end{matrix}\\\end{matrix}\\\end{matrix}\right]$$となる。
FFTのバタフライ演算との類似性がわかりやすいので、他の量子ビットについても変換行列を記載しておく。第2量子ビットについては、
$$\left[\begin{matrix}1&\cdots&1\ &\ &\ &\ &\ &\ \\\vdots&1&\vdots&1\ &\ &\ &\ &\ \\\ 1&\cdots\ &-1&\vdots&\ &\ &\ &\ \\\ &1\ &\cdots\ &-1&\ &\ &\ &\ \\\ &\ &\ &\ &1&\cdots&1&\ \\\ &\ &\ &\ &\vdots&1&\vdots&1\ \\\ &\ &\ &\ &1&\cdots&-1&\vdots\\\ &\ &\ &\ &\ &1\ &\cdots&-1\\\end{matrix}\right]\left[\begin{matrix}a_0\\a_1\\\begin{matrix}a_2\\a_3\\\begin{matrix}a_4\\a_5\\\begin{matrix}a_6\\a_7\\\end{matrix}\\\end{matrix}\\\end{matrix}\\\end{matrix}\right]$$(行列中の…は縦横の並びをわかりやすくするために記載したが、1, -1以外の
要素は全て0になる。)
第3量子ビットについては、
$$\left[\begin{matrix}1&\ &\cdots&\ &\ 1&\ &\ &\ \\\ &1&\ &\cdots&\ &1\ &\ &\ \\\vdots&\ &1&\ &\cdots&\ &1\ &\ \\\ &\vdots\ &\ &1&\ &\cdots&\ &1\ \\\ 1&\ &\vdots&\ &-1&\ &\ &\ \\\ &\ 1&\ &\vdots&\ &-1&\ &\vdots\\\ &\ &\ 1&\ &\ &\ &-1&\ \\\ &\ &\ &1\ &\ &\cdots&\ &-1\\\end{matrix}\right]\left[\begin{matrix}a_0\\a_1\\\begin{matrix}a_2\\a_3\\\begin{matrix}a_4\\a_5\\\begin{matrix}a_6\\a_7\\\end{matrix}\\\end{matrix}\\\end{matrix}\\\end{matrix}\right]$$となる。
*本追記の「1.について」の繰り返しになるが、確認する。第3量子ビットは、演算する前の状態では他の量子ビットから十分切り離されているので、孤立した量子ビットとして \(a\left|0\right\rangle+b\left|1\right\rangle\) と書けるように思われるが、実際には \(\left|0\right\rangle\) 状態は第0、第2、第4、第6量子ビットとの直積になっており(≒量子もつれ状態になっており)、 \(\left|1\right\rangle\) 状態は第1、第3、第5、第7量子ビットとの直積になっている。 \(a_0\) ~ \(a_7\) が全て1のとき等で、他の量子ビットとの量子もつれがない状態(因数分解できる状態)以外では、 \(a\left|0\right\rangle+b\left|1\right\rangle\) のような、量子ビット内だけで閉じた状態として表すことはできない。
(6(このレビュー自身はQECの解説)では、p.69の注で、このことについて、一つのビットを \(a\left|0\right\rangle+b\left|1\right\rangle\) のようにあらわした時、a,bは数字である必要はなく、 \(\left|0\right\rangle\) 、 \(\left|1\right\rangle\) と直交した状態(他の量子ビットの直積の線形結合)であってもよいと書かれている。これで何かイメージできるわけではないが、参考まで。)
2量子ビット演算等に関する補遺
制御Rkについて:
量子演算は、n量子ビットの直積で張られる空間内でのユニタリ変換で、たとえば量子ビットごと、または複数量子ビット間のユニタリ変換等である。
任意の量子演算は、1量子ビット演算H, T, 2量子ビット演算CNOT(制御NOT)の3種類の量子演算の組み合わせで実現できることがわかっている(複数量子ビット間、また、量子ビット内の任意の回転操作(を任意の精度で実現すること)を含めて)。7
前章「「基本的なアイデア」に関する追記」で、直積に対する1ゲート演算子の変換行列について書いたが、2量子ビット演算は量子もつれ状態を生成できる演算であることから、2量子ビットの直積に対する変換行列として表す方が自然である。
2量子ビットの直積の線形結合
$$a_0\left|00\right\rangle+a_1\left|01\right\rangle+a_2\left|10\right\rangle+a_3\left|11\right\rangle$$
に対して、CNOTは
$$\left[\begin{matrix}1&\ &\ &\ \\\ &1&\ &\ \\\ &\ &\ &1\\\ &\ &1&\ \\\end{matrix}\right]\left[\begin{matrix}a_0\\a_1\\\begin{matrix}a_2\\a_3\\\end{matrix}\\\end{matrix}\right]$$
となる。第1量子ビットが
\(\left|0\right\rangle\) のときはそのままで、
\(\left|1\right\rangle\) のときは第2量子ビットがひっくり返る(NOT演算 \(\left[\begin{matrix}\left|0\right\rangle_2\\\left|1\right\rangle_2\\\end{matrix}\right]\rightarrow\left[\begin{matrix}\left|1\right\rangle_2\\\left|0\right\rangle_2\\\end{matrix}\right]\) )。
制御Rkは、上記のように、このCNOTと、H, Tの組み合わせにより実現できる。行列で表現すると、下記のように表される。
$$\left[\begin{matrix}1&\ &\ &\ \\\ &1&\ &\ \\\ &\ &\ 1&\ \\\ &\ &\ &e^\frac{i2\pi}{2^{k+1}}\ \\\end{matrix}\right]\left[\begin{matrix}a_0\\a_1\\\begin{matrix}a_2\\a_3\\\end{matrix}\\\end{matrix}\right]$$2量子ビット演算の物理的な実現方法は8に詳しい。
覚書
調べきれなかった内容の覚書
- 2n点のフーリエ変換には、2-n回転演算が必要になる。演算の回数は対数関数的に減少して、nのオーダーになる。が、回転演算は高い精度が要求されることになる。この演算精度は現状どの程度で、今後どの程度まで改善されるか? RSA暗号に必要な2048ビットの数の素因数分解に必要な演算精度は確保できるか。
- 嶋田義皓 量子コンピューティング オーム社 p.64 ↩︎
- 量子フーリエ変換 (Quantum Fourier Transform) とは – 物理とか ↩︎
- 量子コンピューターで解ける問題はいくつある? | 日経クロステック(xTECH) ↩︎
- 【フーリエ解析05】高速フーリエ変換(FFT)とは?内側のアルゴリズムを解説!【解説動画付き】 ↩︎
- KOUGK378-02_14172.pdf ↩︎
- J. Kempe, Approaches to Quantum Error Correction, S´ eminaire Poincar´ e 1, 65 (2005). kempe.pdf ↩︎
- 嶋田義皓 量子コンピューティング オーム社 p.30 ↩︎
- S. Kwon et al. Tutorial: Gate-based superconducting quantum computing, J. Appl. Phys., 129, 041102 (2021). [2009.08021] Tutorial: Gate-based superconducting quantum computing ↩︎
2025.2.28 公開
2025.5.7 式の入力ミスを訂正